By Quadsoft

Willkommen

Auf dieser Website finden Sie meine Abhandlung zum Thema "Fraktale Geometrie". Diese Arbeit enstand bereits vor mehreren Jahren während des 12. Jahrgangs meiner gymnasialen Oberstufe im Rahmen einer sog. "Besonderen Lernleistung". Ziel war es, eine auch für den Laien verständliche Einführung in dieses äußerst interessante Thema zu gewähren. Da die Arbeit sehr positiv bewertet wurde, entschloss ich mich, sie hier auf meiner Website zu veröffentlichen. Erst vor kurzem hatte ich - nach über sechs Jahren - Zeit, die Arbeit nochmals zu überarbeiten. Es wurden einige Fehler korrigiert und der Text an mehreren Stellen erweitert.

Ich wünsche Ihnen viel Spaß bei der Lektüre und hoffe, dass Sie an diesem sehr spannenden Thema Gefallen finden.

Adrian Jablonski, im Juli 2017

Hier können Sie die im Text erwähnte Software IFS-Generator herunterladen

---

Inhaltsverzeichnis

1 Einleitung

Die fraktale Geometrie ist ein relativ neues Teilgebiet der Mathematik. Sie befasst sich mit geometrischen Objekten, den sog. Fraktalen, deren Eigenschaften sich von denen der "klassischen" Geometrie grundlegend unterscheiden.Wichtigstes Merkmal von Fraktalen ist die Skaleninvarianz, d.h., dass man bei jeder Vergrößerungsstufe Einzelheiten erkennen kann, egal wie stark man in das Objekt hinein dringt. Wenn man dagegen den Rand eines "klassischen" Objektes, wie den des Kreises, vergrößert, so ähnelt dieser mit zunehmender Vergrößerung immer mehr einer schlichten Gerade. Solche Objekte werden demnach als glatt bezeichnet. Bei einem Fraktal wird man jedoch nie eine Gerade erkennen können, sondern immer mehr Feinheiten des Objektes. Daher rührt die Bezeichnung "Fraktal", vom lateinischen "fractus" für "gebrochen", d.h. mit unzähligen Details übersät. Derartige Objekte waren schon seit Anfang des 20. Jahrhunderts bekannt, aber erst ab ca. 1970 wurde deren grundlegende Bedeutung erkannt. Davor wurden diese Objekte als "mathematische Monster" bezeichnet, da sie, wie im Folgenden erläutert wird, paradoxe Eigenschaften besitzen, die dem menschlichen Verstand mehr oder weniger "unbegreiflich" erscheinen. Dies änderte sich erst durch die Arbeit des Mathematikers Benoît Mandelbrot. Er erkannte, dass man mit Fraktalen etwas gänzlich Neues machen konnte, etwas was bis zu dieser Zeit als praktisch mathematisch unmöglich galt: die Modellierung und Beschreibung von "unregelmäßigen" Objekten der Natur, insbesondere der belebten, von der man annahm, sie könne nicht geometrisch beschrieben werden.
In dieser Besonderen Lernleistung witd sich zunächst mit den "klassischen" Fraktalen des 20. Jahrhunderts auseinandergesetzt, um anhand dieser die grundlegenden Konzepte der Fraktalgeometrie zu erläutern. Anschließend stelle werden die sog. iterierten Funktionensysteme (IFS) vorgestellt, ein mächtiges Verfahren zur Kodierung und Generierung von Fraktalen, vor. Dabei wird auf die genaue Definition und deren Verwendung zur Modellierung und Darstellung naturähnlicher Strukturen eingegangen werden. Um die Theorie der Fraktale anschaulich erläutern zu können, habe wurde diese Arbeit mit zahlreichen Bildern, die zum Großteil vom Autor selbst erstellt worden sind, illustriert. Dadurch vergrößert sich zwar der Umfang des Hauptteils, doch ist es fast unmöglich, Geometrie ohne Verwendung von Bildern zu erklären.
Im Rahmen dieser Arbeit ist ebenfalls ein Computerprogramm entstanden, das die Funktionalität der IFS implementiert und anschaulich begreifbar macht. Darüber hinaus befinden sich in dieser Arbeit Ausarbeitungen, die nicht der Literatur entnommen wurde, insbesondere die Flächenformel der Cesàro-Kurve.

2 Begriffe und Definitionen

Um Fraktale und ihre zugrunde liegende Geometrie verstehen zu können, ist es zunächst notwendig, einige mathematische Begriffe zu erläutern, die nicht in der Schulmathematik vermittelt wurden. Ohne die Kenntnis dieser Termini ist eine tief gehende Auseinandersetzung mit den Methoden und Theorien der fraktalen Geometrie nicht möglich. Bedauerlicherweise sind die Themen jedoch derart umfangreich, dass nur die wichtigsten Aspekte behandelt werden können.

2.1 Räume

Der Begriff des Raumes ist in der Mathematik sehr weit gefasst. Daher wird im Folgenden nur auf solche Räume eingegangen, die bereits aus der Schulmathematik bekannt sind bzw. sich einfach daraus herleiten lassen. Beginnen wir mit folgender Definition:

Aus der analytischen Geometrie sind bereits einige Veranschaulichungen solcher Räume bekannt, nämlich das zweidimensionale und das dreidimensionale Koordinatensystem. Aber auch die reelle Zahlengerade ist eine Veranschaulichung eines Raumes, nämlich des Raumes $ℝ$, der der Menge der reellen Zahlen entspricht. Dementsprechend werden der zweidimensionale Raum als ${ℝ}^{\text{2}}$ und der dreidimensionale als ${ℝ}^3$ bezeichnet (${ℝ}^{\text{2}}$ wird auch Euklidische Ebene, nach der Geometrie des Euklid, genannt). Dabei werden die Punkte dieser jeweiligen Räume durch Koordinaten dargestellt, die Anzahl der Koordinaten ist gleich der Dimension, d.h. der "räumlichen Ausdehnungen" des Raumes, die sich im Exponenten nach dem $ℝ$ widerspiegeln; so hat ein beliebiger Punkt im Raum ${ℝ}^{\text{2}}$ die Koordinaten $\left(x|y\right)$ und in ${ℝ}^3$$\left(x\left|y\right|z\right)$, wobei $x,y,z\in ℝ$gilt. Die obige Definition impliziert (obwohl es nicht explizit gesagt ist), dass definiert ist, wie die Punkte im Raum anzuordnen sind und wie sie zueinander in Beziehung stehen. Ein Raum kann aber auch eine ganz andere "Art" von Menge sein als die hier vorgestellten Beispiele, z.B. können die Punkte eines Raumes ganze Funktionen sein, die eine bestimmte Eigenschaft besitzen (z.B. der Raum $X$ aller differenzierbaren Funktionen, ein Punkt dieses Raumes wäre dann z.B. $f\left(x\right)=x\text{²},f\in X$). Im Folgenden wird auf die genauere Klassifikation von Räumen eingegangen.

2.1.1 Vektorräume

Ein Vektorraum V (oder linearer Raum) ist ein Raum, dessen Punkte als Vektorenbezeichnet werden, wenn Folgendes gilt:

1. Die Addition zweier Punkte ergibt wiederum einen Punkt des Raumes, formal: für alle $\overrightarrow{a},\overrightarrow{b}\in V$ gilt: $\overrightarrow{a}+\overrightarrow{b}\in V$.
2. Die Skalarmultiplikation ergibt wiederum einen Punkt des Raumes, formal: für alle $r\in ℝ,\overrightarrow{a}\in V$ gilt: $r\cdot \overrightarrow{a}\in V$.

Somit sind $ℝ$, ${ℝ}^{\text{2}}$ und ${ℝ}^3$Beispiele für Vektorräume, da beide Bedingungen erfüllt sind. Ein Vektorraum kann aber auch eine beliebige andere Menge sein, auf die die obigen Bedingungen zutreffen.

Beispiel

am Raum ${ℝ}^{\text{2}}$:

$$\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 2\hfill \end{array}\right)+\left(\begin{array}{c}\hfill 3\hfill \\ \hfill 4\hfill \end{array}\right)=\left(\begin{array}{c}\hfill 4\hfill \\ \hfill 6\hfill \end{array}\right)\text{ und }3\cdot \left(\begin{array}{c}\hfill 1\hfill \\ \hfill 2\hfill \end{array}\right)=\left(\begin{array}{c}\hfill 3\hfill \\ \hfill 6\hfill \end{array}\right)$$

2.1.2 Metrische Räume

Nun kommen wir zu einer Art von Räumen, die für das Verständnis der fraktalen Geometrie von entscheidender Bedeutung sind.
Unter einem metrischen Raum $\left(X,d\right)$ versteht man einen gegebenen Raum $X$(z.B. den Vektorraum ${ℝ}^{\text{2}}$), der mit einer sog. Metrik $d$ versehen ist. Eine Metrik $d\left(x,y\right)$ ist eine Funktion, die den Abstand zwischen zwei gegebenen Punkten $x,y\in X$angibt. Diese Funktion darf aber nicht beliebig sein, sondern muss folgende Eigenschaften besitzen:

1. Für den Abstand zweier Punkte muss gelten (es muss eine Symmetrie vorhanden sein): $d\left(x,y\right)=d\left(y,x\right)$für alle $x,y\in X$
2. Der Abstand zwischen zwei unterschiedlichen Punkten darf nicht unendlich groß oder 0 sein, formal: $0<d\left(x,y\right)<\infty$ für alle $x,y\in X$wenn $x\ne y$.
3. Der Abstand identischer Punkte muss 0 sein, formal: $d\left(x,x\right)=0$ für alle $x\in X$
4. Die Dreiecksungleichung (In einem beliebigen Dreieck gilt: "Die Summe der Längen der Seiten a und b ist größer oder gleich der Länge der Seite c, d.h.$c\le a+b$") muss erfüllt sein:
   $d\left(x,y\right)\le d\left(x,z\right)+d\left(z,y\right)$für alle $x,y,z\in X$

Aus der Schulmathematik ist bereits eine solche Metrik bekannt, ohne sie explizit als solche aufgefasst zu haben, nämlich der Abstand zwischen zwei Punkten als Betrag des Vektors von A nach B:

$$d_E\left(A,B\right)=\left|\overrightarrow{AB}\right|=\sqrt{{\left(a_x-b_x\right)}^2+{\left(a_y-b_y\right)}^2}\mathrm{\text{für alle }}A,B\in {ℝ}^2$$

(1)

und

$$d_E\left(A,B\right)=\left|\overrightarrow{AB}\right|=\sqrt{{\left(a_x-b_x\right)}^2+{\left(a_y-b_y\right)}^2+{\left(a_z-b_z\right)}^2}\mathrm{\text{für alle }}A,B\in {ℝ}^3.$$

(2)

Diese Metrik wird als die Euklidische Metrik bezeichnet. Eine weitere Metrik ist z.B. die sog. Gittermetrik bzw. Manhattanmetrik:

$$d_g\left(A,B\right)=|a_x-b_x|+|a_y-b_y|\mathrm{\text{ für alle }}A,B\in {ℝ}^2$$

(3)

und

$$d_g\left(A,B\right)=|a_x-b_x|+|a_y-b_y|+|a_z-b_z|\mathrm{\text{ für alle }}A,B\in {ℝ}^3$$

(4)

---

---

Diese Metrik gibt nicht mehr den kürzesten direkten Abstand an, sondern die Länge des Weges über die Maschen eines gedachten Gitters, ähnlich der Straßenanordnung in Manhattan (daher der Name Manhattanmetrik). Es gibt unzählige Arten von Metriken, aber nicht alle haben eine so intuitive Begreifbarkeit wie die bereits vorgestellten. So gibt es die sog. diskrete Metrik, deren Definition relativ abstrakt ist und keinerlei praktische Veranschaulichung bietet (sie kann auf beliebige Räume angewendet werden):

$$d_d\left(A,B\right)=\left\{\begin{array}{cc}\begin{array}{c}\hfill 0\mathrm{\text{ für }}A=B\hfill \\ \hfill 1\mathrm{\text{ für }}A\ne B\hfill \end{array}\hfill & \mathrm{\text{für alle }}A,B\in X\hfill \end{array}\right.$$

(5)

Bei der diskreten Metrik beträgt der Abstand identischer Punkte also 0 und unterschiedlicher Punkte 1. Diese Metrik ist eher eine theoretische Spielerei, um zu zeigen, dass auch sehr abstrakte Funktionen die vier Eigenschaften einer Metrik erfüllen können.

2.2 Affine Abbildungen

Eine Abbildung ist allgemein eine Funktion $f$, die einen Raum $X$ auf einen Raum $Y$ abbildet, formal $f:X\to Y$, dabei wird jeder Punkt des Raumes $X$ auf einen Punkt des Raumes $Y$ abgebildet. Für die fraktale Geometrie sind eine spezielle Art von Abbildungen, sog. affine Abbildungen, für das Verständnis unbedingt notwendig. Eine affine Abbildung bildet einen Punkt eines beliebigen Vektorraumes auf einen anderen Punkt desselben Raumes ab. Wir beschränken uns hierbei auf den Raum ${ℝ}^2$. Eine affine Abbildung $w$ hat demnach die allgemeine Form

$$w:{ℝ}^2\to {ℝ}^2.$$

(6)

Affine Abbildungen ordnen einem Urbildpunkt $P\in {ℝ}^2$ genau einen Bildpunkt $P^{\prime }\in {ℝ}^2$ zu, man nennt eine solche Abbildung eineindeutig bzw. bijektiv. Aus der Schulgeometrie sind bereits einige affine Abbildungen bekannt, darunter die Ähnlichkeitsabbildungen, wie z.B. die zentrische Streckung. Zu den affinen Abbildungen zählen insgesamt die Translation (Verschiebung), die Skalierung, die Rotation (Drehung), die Spiegelung und die Transvektion (Scherung). Alle diese Abbildungen und deren Kombinationen lassen sich durch eine Matrix $A$ und einen Verschiebungsvektor $\overrightarrow{v}$ darstellen:

$$A=\left(\begin{array}{cc}\hfill a\hfill & \hfill b\hfill \\ \hfill c\hfill & \hfill d\hfill \end{array}\right),\overrightarrow{v}=\left(\begin{array}{c}\hfill e\hfill \\ \hfill f\hfill \end{array}\right)$$

Zusammengefasst lässt sich eine affine Abbildung $w$ durch die Formel

$$w:\overrightarrow{p^{\prime }}=A\overrightarrow{p}+\overrightarrow{v}$$

(7)

$$w:\left(\begin{array}{c}\hfill p_x^{\prime }\hfill \\ \hfill p_y^{\prime }\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill a\hfill & \hfill b\hfill \\ \hfill c\hfill & \hfill d\hfill \end{array}\right)\cdot \left(\begin{array}{c}\hfill p_x\hfill \\ \hfill p_y\hfill \end{array}\right)+\left(\begin{array}{c}\hfill e\hfill \\ \hfill f\hfill \end{array}\right)$$

(8)

beschreiben. Um nun die Koordinaten eines Punktes zu berechnen, muss man zunächst die Matrizenmultiplikation

$$A\cdot \overrightarrow{x}=\left(\begin{array}{cc}\hfill a\hfill & \hfill b\hfill \\ \hfill c\hfill & \hfill d\hfill \end{array}\right)\cdot \left(\begin{array}{c}\hfill p_x\hfill \\ \hfill p_y\hfill \end{array}\right)=\left(\begin{array}{c}\hfill a\cdot p_x+b\cdot p_y\hfill \\ \hfill c\cdot p_x+d\cdot p_y\hfill \end{array}\right)$$

ausführen. Anschließend addiert man $\overrightarrow{v}$ und erhält

$$\begin{array}{c}\hfill p_x^{\prime }=a\cdot p_x+b\cdot p_y+e\hfill \\ \hfill p_y^{\prime }=c\cdot p_x+d\cdot p_y+f\hfill \end{array}$$

für die beiden Koordinaten des Bildpunktes $P^{\prime }$.
Nun wird erläutert, wie man durch die Matrizendarstellung alle oben erwähnten Abbildungen beschreiben kann.

---

---

2.2.1 Translation

Die Translation $w_t$ um einen Vektor

$$\overrightarrow{v}=\left(\begin{array}{c}\hfill v_x\hfill \\ \hfill v_y\hfill \end{array}\right)$$

ist die Verschiebung eines Objekts um genau diesen Vektor. Da bei der Matrizenmultiplikation die Ursprungskoordinaten erhalten bleiben sollen, muss es sich bei der Abbildungsmatrix um die Einheitsmatrix handeln. Somit erhält man:

$$w_t:\left(\begin{array}{c}\hfill p_x^{\prime }\hfill \\ \hfill p_y^{\prime }\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)\cdot \left(\begin{array}{c}\hfill p_x\hfill \\ \hfill p_y\hfill \end{array}\right)+\left(\begin{array}{c}\hfill v_x\hfill \\ \hfill v_y\hfill \end{array}\right)$$

(9)

Diese Abbildung verschiebt also den Punkt $P^{\prime }$um den Vektor $\overrightarrow{v}$.

Beispiel

Verschiebung von $A\left(3|6\right)$ um$\overrightarrow{v}=\left(\begin{array}{c}\hfill 2\hfill \\ \hfill 3\hfill \end{array}\right)$:

$$\overrightarrow{a^{\prime }}=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)\cdot \left(\begin{array}{c}\hfill 3\hfill \\ \hfill 6\hfill \end{array}\right)+\left(\begin{array}{c}\hfill 2\hfill \\ \hfill 3\hfill \end{array}\right)=\left(\begin{array}{c}\hfill 3+0+2\hfill \\ \hfill 0+6+3\hfill \end{array}\right)=\left(\begin{array}{c}\hfill 5\hfill \\ \hfill 9\hfill \end{array}\right)$$

Die Koordinaten von $A^{\prime }$ lauten demnach $A^{\prime }\left(5|9\right)$.

2.2.2 Skalierung

Eine Skalierung $w_s$ ist eine Größenänderung eines Objektes, z.B. eines Rechtecks. Dabei kann dies in $x$- und bzw. oder in $y$-Richtung geschehen. Ein Objekt wird skaliert, indem man eine affine Abbildung der Form (der Verschiebungsvektor wurde der Übersichtlichkeit wegen weggelassen)

$$w_s=\left(\begin{array}{c}\hfill p_x^{\prime }\hfill \\ \hfill p_y^{\prime }\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill a\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill b\hfill \end{array}\right)\cdot \left(\begin{array}{c}\hfill p_x\hfill \\ \hfill p_y\hfill \end{array}\right);a,b\in {ℝ}_{+}^{*}$$

(10)

verwendet. Dabei skalieren der Faktor $a$ in $x$-Richtung und der Faktor $b$  in $y$-Richtung.

Beispiel

Skalierung des Dreiecks ${\Delta }_{ABC}\mathrm{\text{ mit }}A=\left(0|1\right),B=\left(0|\text{0}\right)\mathrm{\text{ und}}C=\left(1|0\right)$ auf $0,5$ in $x$- und $y$-Richtung:

Die affine Abbildung dazu lautet

$$w_s=\left(\begin{array}{c}\hfill p_x^{\prime }\hfill \\ \hfill p_y^{\prime }\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill 0,5\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0,5\hfill \end{array}\right)\cdot \left(\begin{array}{c}\hfill p_x\hfill \\ \hfill p_y\hfill \end{array}\right)$$

Somit lauten die Koordinaten des neuen Dreiecks $A^{\prime }\left(0|0,5\right),B^{\prime }\left(0|0\right)\mathrm{\text{ und }}{C}^{\prime }\left(0,5|0\right)$.

2.2.3 Rotation

Als nächstes wird die Rotation $w_r$ behandelt, zunächst nur um den Ursprung, dann um einen beliebigen Punkt $Q$. Um einen Punkt $P$ mit einen Winkel $\alpha$ gegen den Uhrzeigersinn um den Ursprung $O\left(0|0\right)$ zu drehen, verwendet man eine Abbildungsmatrix $R$ (Rotationsmatrix) der Form

$$R=\left(\begin{array}{cc}\hfill cos\alpha \hfill & \hfill -sin\alpha \hfill \\ \hfill sin\alpha \hfill & \hfill cos\alpha \hfill \end{array}\right)$$

(11)

Um nun eine Rotation um einen beliebigen Punkt $Q=\left(q_x|q_y\right)$ durchzuführen, muss man den zu drehenden Punkt $P$ und den Punkt $Q$ derart verschieben, dass $Q$ auf $O$ fällt. Dazu verschiebt man $P$ einfach um

$$-q=-\left(\begin{array}{c}\hfill q_x\hfill \\ \hfill q_y\hfill \end{array}\right)$$

Nun kann man die gewohnte Rotationsmatrix anwenden. Anschließend muss man $P$ an den Ausgangspunkt zurückversetzen. Zusammengefasst ergibt dies

$$\overrightarrow{p^{\prime }}=A\cdot \left(\overrightarrow{p}-\overrightarrow{q}\right)+\overrightarrow{q}$$

2.2.4 Weitere affine Abbildungen

Auf die weiteren Arten von affinen Abbildungen wie Scherung und Spiegelung wird nicht weiter eingegangen, da die bereits beschriebenen Arten für das Verständnis ausreichend sind. Erstere lassen sich aber ebenfalls durch die Elemente der Abbildungsmatrix und einen Verschiebungsvektor darstellen.

2.2.5 Verkettung affiner Abbildungen

Um z.B. erst eine Rotation $\alpha$ und anschließend eine Skalierung $\beta$, also $\beta \left(\alpha \left(\overrightarrow{x}\right)\right)$, durchzuführen, lassen sich zwei affine Abbildungen $\alpha :\overrightarrow{x^{\prime }}=A\cdot \overrightarrow{x}$ und $\beta :\overrightarrow{x^{\prime }}=B\cdot \overrightarrow{x}$ miteinander verknüpfen, indem man die Matrix $A$ mit der Matrix $B$ und anschließend mit $\overrightarrow{x}$ multipliziert. Für die Verkettung verwendet man das Symbol $\circ$. Der Ausdruck $\alpha \circ \beta$ bedeutet, dass erst $\beta$ und dann $\alpha$ angewendet wird, d.h. $\alpha \left(\beta \left(\overrightarrow{x}\right)\right)$. Für das obige Beispiel ergibt sich daher $\overrightarrow{x^{\prime }}=B\cdot A\cdot \overrightarrow{x}=\beta \circ \alpha$. Zu beachten ist, dass die Matrizenmultiplikation nicht kommutativ ist, also in der Regel $A\cdot B\ne B\cdot A$ gilt.

2.2.6 Berechnung einer affinen Abbildung

Eine affine Abbildung lässt sich durch jeweils drei gegebene Bild- und Urbildpunkte $\overrightarrow{x},\overrightarrow{y},\overrightarrow{z}$,
${\overrightarrow{x}}^{\prime },{\overrightarrow{y}}^{\prime },{\overrightarrow{z}}^{\prime }$ berechnen. Dazu nutzt man die Tatsache, dass

$$\left(\begin{array}{cc}\hfill a\hfill & \hfill b\hfill \\ \hfill c\hfill & \hfill d\hfill \end{array}\right)\left(\begin{array}{c}\hfill p_x\hfill \\ \hfill p_y\hfill \end{array}\right)+\left(\begin{array}{c}\hfill e\hfill \\ \hfill f\hfill \end{array}\right)=\left(\begin{array}{c}\hfill p_x^{\prime }\hfill \\ \hfill p_y^{\prime }\hfill \end{array}\right)$$

gilt und man somit zwei lineare Gleichungssysteme

$\begin{array}{c}\hfill x_{x}a+x_{y}b+e=x_x^{\prime }\hfill \\ \hfill y_{x}a+y_{y}b+e=y_x^{\prime }\hfill \\ \hfill z_{x}a+z_{y}b+e=z_x^{\prime }\hfill \end{array}$und   $\begin{array}{c}\hfill x_{x}c+x_{y}d+f=x^{\prime }\hfill \\ \hfill y_{x}c+y_{y}d+f=y_y^{\prime }\hfill \\ \hfill z_{x}c+z_{y}d+f=z_y^{\prime }\hfill \end{array}$

(12)

aufstellen kann. Durch Lösen dieser LGS erhält man die Elemente der Abbildungsmatrix $a,b,c,d$ und die Komponenten des Translationsvektors $e,f$  der entsprechenden Abbildung $w$, die $\overrightarrow{x},\overrightarrow{y}$ und $\overrightarrow{z}$ auf $\overrightarrow{x^{\prime }},\overrightarrow{y^{\prime }}$ und $\overrightarrow{z^{\prime }}$ abbildet. Wählt man willkürlich beliebige Bild- und Urbildpunkte, so erhält man in der Regel eine Verkettung verschiedener affiner Abbildungen.

2.2.7 Fixpunkte affiner Abbildungen

Ein Fixpunkt $P$ ist ein Punkt, der bei Anwendung einer affinen Abbildung invariant (unverändert) bleibt, d.h. dass $f\left(\overrightarrow{p}\right)=\overrightarrow{p}$ gilt. Fixpunkte lassen sich mit Hilfe der Formeln

$$x=\frac{-e\left(d-1\right)+bf}{\left(a-1\right)\left(d-1\right)-bc},y=\frac{-f\left(a-1\right)+ce}{\left(a-1\right)\left(d-1\right)-bc}$$

(13)

berechnen. ($a,b,c,d$ sind die Elemente der Abbildungsmatrix und $e,f$ die Komponenten des Translationsvektors.)

2.2.8 Eigenschaften affiner Abbildungen

Je nach ihren Eigenschaften lassen sich affine Abbildungen in folgende Gruppen einteilen:

• Kongruenzabbildungen (umfassen Spiegelungen, Translationen und Rotationen sowie deren Verkettungen)
  • Abgebildete Objekte sind zum Urbild deckungsgleich (kongruent), d.h., dass Form und Größe des Bildes der des Urbilds entspricht.
  • Daraus folgt: Parallelität, Flächeninhalt, Flächenverhältnisse, Winkel, Längen und Längenverhältnisse bleiben invariant.
• Ähnlichkeitsabbildungen (umfassen Kongruenzabbildungen sowie Skalierungen und deren Verkettungen)
  • Parallelität, Winkel, Flächenverhältnisse und Längenverhältnisse bleiben invariant.
• Affine Abbildungen (umfassen Kongruenzabbildungen, Ähnlichkeitsabbildungen sowie Scherungen und deren Verkettungen)
  • Parallelität, Flächenverhältnisse und Längenverhältnisse bleiben invariant.

2.2.9 Kontraktionen

Eine Kontraktion ist eine besondere Art von (affinen) Abbildungen. Eine unendliche Anwendung dieser bewirkt, dass ein beliebiger metrischer Raum $X$ auf einen einzigen Punkt zusammengezogen wird. Dieser Punkt ist zugleich der einzige Fixpunkt dieser (affinen) Abbildung. ¹ Die Kontraktion verursacht demnach eine Stauchung aller Mengen, die in dem Raum eingebettet sind. Für eine Kontraktion $w:X\to X$ gilt folglich

$$d\left(w\left(x\right),w\left(y\right)\right)\le s\cdot d\left(x,y\right)\mathrm{\text{für alle }}x,y\in X.$$

(14)

Dabei wird $s$ als Kontraktionsfaktor bezeichnet. Er gibt an, wie "stark" der Raum gestaucht wird. Ob eine Abbildung eine Kontraktion ist, hängt offensichtlich davon ab, bezüglich welcher Metrik $d$ man sie betrachtet. Beispielsweise gibt es Metriken, die bezüglich der Euklidischen Metrik Kontraktionen sind, bezüglich der Gittermetrik aber nicht.

---

---

2.3 Dimension

Dimension ist ein zentraler Begriff in der fraktalen Geometrie, wo er als Maß für die "Gebrochenheit" von Objekten dient. Um dies verstehen zu können, muss zunächst geklärt werden, was in der "klassischen" Geometrie darunter verstanden wird.
Prinzipiell gibt die einbettende Dimension eines Vektorraumes an, wie viele Ausdehnungen (oder Freiheitsgrade) dieser besitzt. Diese ist gegeben durch die Anzahl der Koordinaten des Vektors, so hat ein Vektor des Raumes ${ℝ}^{\text{2}}$ zwei Koordinaten $\overrightarrow{x}=\left(\begin{array}{c}\hfill x_1\hfill \\ \hfill x_2\hfill \end{array}\right)$. Dementsprechend hat der Raum ${ℝ}^{\text{3}}$ die Dimension drei. ² Dimensionen kann man aber nicht nur für Räume, sondern auch für darin eingebettete Objekte, die dann als Teilmenge des Raumes bezeichnet werden, bestimmen. Befindet sich z.B. eine Gerade in der Ebene, so hat diese die Dimension 1, da sie nur eine Ausdehnung besitzt (sie ist unendlich lang, aber auch unendlich dünn.). Ein Punkt dagegen hat die Dimension 0.

2.3.1 Topologische Dimension

Um die Dimension einer Teilmenge genau zu bestimmen, wurde die sog. topologische Dimension eingeführt. Sie entspricht der "intuitiven" Dimension, die man einer Teilmenge anschaulich zuordnen kann. Zunächst wird grob geklärt, was überhaupt unter "Topologie" verstanden wird: Die Topologie ist ein Teilgebiet der Mathematik, das sich mit Objekten befasst, die sich in einem "gummiartigen" Raum befinden, d.h., dass diese durch bestimmte Abbildungen beliebig transformiert ("verzerrt") werden können. Diese Abbildungen werden als Homöomorphismen bezeichnet. Die "Verzerrungen", die sie beschreiben, sind jedoch nicht beliebig, sondern lassen Löcher und Verbindungsstellen invariant. So gibt es Homöomorphismen, die eine Gerade in eine gezackte bzw. "zerknüllte" Linie transformieren. Solche Objekte, die durch Homöomorphismen ineinander übergehen können, bezeichnet man als homöomorph oder topologisch äquivalent. Demnach sind z.B. auch eine glatte Kugel und ein "kartoffelartiges" Gebilde homöomorph. Nicht homöomorph wäre dagegen die Kugel mit einem Torus, da dieser ein Loch enthält.
Um nun die Dimensionen von Teilmengen zu bestimmen, hat der französische Mathematiker Henri Lebesgue folgende sehr anschauliche Definition ³ auf Basis der Topologie entwickelt:
Es soll versucht werden, die gegebene Menge durch kleine Kugeln oder Kreisscheiben derart komplett zu überdecken, dass die Anzahl an Überschneidungen $n$ zwischen diesen minimal wird. Die Dimension der Menge beträgt dann $n-1$. Ein Beispiel: Die Dimension eines Punktes ist 0, weil er bereits durch eine Kreisscheibe beliebigen Radius überdeckt werden kann. Ebenso verfährt man mit Geraden. Hier ist die minimale Überschneidung zwei, daher ist sie eindimensional. Diese Dimension ergibt sich aber folglich auch für z.B. für eine Kurve oder den Rand einer Acht. All diese Objekte sind demnach topologisch betrachtet eindimensional.

---

---

3 Klassische Fraktale

Nachdem die mathematischen Grundlagen behandelt wurden, kann nun begonnen werden, sich dem zentralen Thema dieser Arbeit zu widmen. Zunächst ist aber zu klären, was überhaupt unter einem Fraktal zu verstehen ist.

3.1 Was ist ein Fraktal?

Bei Fraktalen handelt es sich um komplexe geometrische Figuren, deren Struktur stark "gebrochen" (lat. "fractus", daher der Name "Fraktal") bzw. "zerklüftet" erscheint und die einen hohen Grad an Skaleninvarianz aufweisen. Dies bedeutet, dass bei Vergrößerung eines Ausschnitts eines Fraktales stets immer feinere Strukturen erkennbar sind, egal wie stark der Vergrößerungsfaktor ist, man sagt dazu auch, das Fraktal habe "Details auf allen Stufen". Diese Eigenschaft unterscheidet Fraktale von den Objekten der "klassischen" Geometrie, wo bei hinreichender Vergrößerung, z.B. des Randes eines Kreises, eine Gerade erkennbar ist, was in Übrigen die Differenzierbarkeit dieser Objekte, also die Bestimmung der Steigung in einem Punkt, z.B. von Funktionsgraphen, überhaupt ermöglicht. ⁴ Die skaleninvarianten Fraktale dagegen lassen die Bestimmung der Steigung in keinem ihrer Punkte zu.
Dies ist die grundlegende Eigenschaft, die alle Fraktale verbindet. Darüber hinaus gibt es einige spezifische Eigenschaften, auf die weiter unten eingegangen wird. Zunächst werden einige der sog. klassische Fraktale vorgestellt. Sie wurden Ende des 19. bis Anfang des 20. Jahrhunderts entwickelt und von den Mathematikern als "mathematische Monster" bezeichnet, weil sie sich grundsätzlich von den bisherigen Objekten der Geometrie unterschieden.
Formal handelt es sich bei Fraktalen um kompakte ⁵ Teilmengen eines vollständigen ⁶ metrischen Raumes. Der Raum, auf den die Metrik definiert ist, kann z.B. $ℝ$, ${ℝ}^2$ oder ${ℝ}^3$ sein. Im Folgenden beschränken wir uns aber auf den Vektorraum ${ℝ}^2$.

---

---

3.2 Die Koch-Kurve

Die Koch-Kurve (nach dem schwedischen Mathematiker Helge von Koch) ist eines der bekanntesten Fraktale überhaupt. Von Koch stellte sie als Kurve vor, die überall stetig, aber nirgends differenzierbar ist, da sie praktisch nur aus "Ecken" besteht, die keine eindeutige Tangente zulassen.
Zunächst wird die Konstruktion dieser Kurve erläutert: Die Koch-Kurve entsteht, indem man einen sog. Initiator, d.h. ein Ausgangsobjekt, in diesem Fall eine Strecke der Länge 1, drittelt und anschließend den mittleren Teil durch zwei Kopien dieses Drittels ersetzt, sodass diese in einem Winkel von $\alpha =\frac{\pi }{3}$ zueinander und zur Initiatorstrecke stehen. Diesen Schritt, der als Generator bezeichnet wird, wendet man anschließend auf alle vier entstandenen Teilstrecken an, und wiederholt (iteriert) dies (theoretisch) unendlich oft. Das Fraktal, das bei diesem Prozess entsteht, hat besondere Eigenschaften, auf die im Folgenden genauer eingehen werden wird. Es folgt nun ein Bild, das diesen Konstruktionsprozess verdeutlichen soll.

---

---

Wie man leicht erkennen kann, erhöht sich die Anzahl an Ecken pro Iterationsschritt $n$ um $4^{n-1}$, sodass die Grenzkurve, wie bereits oben erwähnt, aus unendlich vielen Ecken - und zwar ausschließlich aus Ecken - zusammengesetzt ist, was nur daher kein Paradoxon ist, da der Konstruktionsprozess unendlich oft iteriert wird. Diese bemerkenswerte Eigenschaft macht sie daher an keiner Stelle differenzierbar.

3.2.1 Selbstähnlichkeit der Koch-Kurve

Selbstähnlichkeit bedeutet, dass ein Objekt aus verkleinerten Kopien seines selbst zusammengesetzt ist, die durch die Anwendung einer kontrahierenden Ähnlichkeitsabbildung entstanden sind. Viele (aber längst nicht alle) Fraktale sind selbstähnlich, und die Koch-Kurve ist ein typisches Beispiel dafür. Betrachtet man sie genau, so erkennt man leicht, dass sie aus vier auf $\frac{1}{3}$ skalierten Teilen aufgebaut ist, von denen der zweite um $\theta =-\frac{\pi }{3}$ und der dritte Teil um $\theta =\frac{\pi }{3}$ rotiert worden ist. Nimmt man nun einen dieser Teile und vergrößert ihn auf das Dreifache, so erhält man wiederum die gesamte Kurve. Dabei setzt sich die Selbstähnlichkeit bei jeder beliebiger Vergrößerungsstufe fort, die Skaleninvarianz der Koch-Kurve ist demnach eine direkte Folge ihrer Selbstähnlichkeit. Es ist jedoch zu beachten, dass kein Konstruktionsschritt der Kurve selbstähnlich bzw. skaleninvariant ist. Theoretisch wäre es nämlich möglich, diesen derart stark zu vergrößern, sodass die Details verschwinden würden und man die eckige Struktur erkennen könnte. Die Selbstähnlichkeit bezieht sich daher nur auf das Grenzobjekt, das nach (theoretisch) unendlich vielen Iterationen entsteht.

---

---

3.2.2 Die Länge der Koch-Kurve

Nun möchte wird gezeigt, wie man die Länge der Koch-Kurve bestimmen kann. Wie bereits erwähnt, hat die Initiatorstrecke die Länge 1. Da der Generator diese durch $a_1=4$ Teilstrecken der Länge $l_1=\frac{1}{3}$ ersetzt, beträgt die Länge der Kurve $L$ während der ersten Iteration $L_1=\frac{4}{3}$. Bei der zweiten Iteration verkürzt sich die Länge der Teilstrecken auf $l_2=\frac{1}{3}\cdot \frac{1}{3}={\left(\frac{1}{3}\right)}^2$ , deren Anzahl steigt jedoch auf $a_2=4\cdot 4=4^2$ und deren Gesamtlänge lautet demnach $L_2={\left(\frac{4}{2}\right)}^2$. Für die dritte Iteration gilt $l_3={\left(\frac{1}{3}\right)}^3$ , $a_3=4^3$ und $L_3={\left(\frac{4}{3}\right)}^3$. Daraus lässt sich folgern, dass für jeden beliebigen Teilschritt $n$ $l_n={\left(\frac{1}{3}\right)}^n$ , $a_n=4^n$ und $L_n={\left(\frac{4}{3}\right)}^n$ gilt, d.h. dass die Gesamtlänge pro Iteration um $\frac{3}{4}$ zunimmt. Da das Konstruktionsverfahren unendlich oft wiederholt wird, ergibt sich für die Koch-Kurve eine Länge von

$$L_{\infty }=\underset{n\to \infty }{lim}{\left(\frac{4}{3}\right)}^n=\infty .$$

(15)

Die Koch-Kurve hat also eine unendliche Länge! Zwar belegt sie eine endliche Fläche, ⁷ da man sie ja auf einem Blatt Papier darstellen kann (wenn auch nur ungenügend), ist sie dennoch von einer gänzlich anderen Natur wie andere bekannte Objekte wie z.B. der Kreis, der nachweislich einen endlichen Umfang und eine endliche Fläche besitzt. Dies ist der Grund, warum die Koch-Kurve und die anderen klassischen Fraktale als "Monster" bezeichnet wurden: Sie entsprachen nun mal nicht den gängigen Vorstellungen geometrischer Objekte.

3.3 Die Cesàro-Kurve

Bei der Cesàro-Kurve handelt es sich um eine Verallgemeinerung der Koch-Kurve. Zwar bleibt der Initiator die Einheitsstrecke, jedoch ändert sich der Generator dahin gehend, dass der Basiswinkel des von der Kurve umschlossenen gleichschenkligen Dreiecks, der bei der Koch-Kurve $\theta =\frac{\pi }{3}$ beträgt, variabel im Bereich von $\theta =0\mathrm{\text{ bis }}\theta =\frac{\pi }{2}$ wird. Dadurch ändert sich folglich der Verkleinerungsfaktor in Abhängigkeit von $\theta$. Im Folgenden wird eine Zusammenstellung von verschiedenen Cesàro-Kurven im Bereich von $\theta =0$ bis $\theta =\frac{\pi }{2}$ in Schritten von $\frac{\pi }{18}$ gezeigt. Für $\theta =0$ ergibt sich die nicht-fraktale Einheitsstrecke, da es keine Längenzunahme wie bei den andren Fällen gibt. Ansonsten sind alle Cesàro-Kurven wie die Koch-Kurve unendlich lang, der Zuwachs an Länge pro Iteration ist aber offensichtlich von $\theta$ abhängig. Da es sich bei $\theta$ um einen Parameter handelt, bilden alle Cesàro-Kurven eine sog. Kurvenschar.

---

---

Man erkennt auf den ersten Blick, dass die Kurve mit zunehmendem $\theta$ immer "rauer" erscheint und immer mehr Fläche "umschließt", bis sie schließlich bei $\theta =\frac{\pi }{2}$ ein gleichschenkliges Dreieck mit einer Fläche von $\frac{1}{4}$ komplett ausfüllt. Dies scheint zunächst paradox, da es sich ja um eine Kurve, also ein Objekt mit der topologischen Dimension 1 handelt, das aber eine Fläche, also ein zweidimensionales Objekt, bildet.

3.3.1 Die fraktale Dimension $D$ der Cesàro-Kurve

Wie es nun scheint, reicht die intuitive Vorstellung, die Cesàro-Kurve als eindimensional zu betrachten, nicht aus. Für zunehmende Werte $\theta$ von scheint sie immer mehr "zerklüftet" zu sein und sich immer mehr einer Fläche anzunähern, also praktisch von "eindimensional zu zweidimensional" zu wechseln. Wie kann man nun ein solches Fraktal charakterisieren? Wenn man die Länge der Kurve $u$ mit einer Genauigkeit von $\frac{1}{s}$ misst, ⁸ ergibt sich ein Potenzgesetz der Form $u\propto {\left(\frac{1}{s}\right)}^D$, jedoch strebt die Länge bei zunehmender Genauigkeit gegen unendlich. Interessant ist aber, dass dabei der Exponent $D$ stets konstant bleibt, wodurch man $D+1$ als Dimension der Kurve annehmen kann. Beispielsweise erhält man für die Koch-Kurve $D\approx 0,26$. Nur ergibt sich dadurch jedoch ein Problem: Bisher waren nur Zahlen aus $\mathbb{N}$ als Dimensionswerte erlaubt. Dies führte den französisch-polnischen Mathematiker Benoît Mandelbrot zu einem radikalen Umändern des Dimensionsbegriffs für derartige Objekte: Er erweiterte den Bereich auf ${ℝ}_{+}$, d.h., dass Dimensionen auch gebrochene Werte annehmen können (eine solche Dimension bezeichnet man daher als fraktale Dimension $D$). Dazu verwendete Mandelbrot die sog. Hausdorff-Besicovitch-Dimension $D_H$, die bereits zuvor von dem deutschen Mathematiker Felix Hausdorff entwickelt und von Abram S. Besicovitch verfeinert wurde. Sie wurde ursprünglich nur für "klassische" Objekte angewandt, doch Mandelbrot erkannte, dass sie sich ideal zur Charakterisierung von Fraktalen eignet. Leider ist die Definition der Hausdorff-Besicovitch-Dimension derart komplex, dass sie den Rahmen dieser Arbeit sprengen würde. Stattdessen kann man sich auf zwei andere Definitionen von fraktalen Dimensionen beschränken, die sich direkt aus der Hausdorff-Besicovitch-Dimension herleiten lassen: zum Einen die Selbstähnlichkeitsdimension $D_S$ und zum Anderen die Box-Dimension $D_B$, die im nächsten Abschnitt behandelt wird.
Die Selbstähnlichkeitsdimension setzt voraus - wie bereits der Name vermuten lässt -, dass das zu untersuchende Objekt (es muss nicht unbedingt ein Fraktal sein) selbstähnlich ist. Sie lässt sich daher aus den bekannten Objekten, deren Dimension man intuitiv kennt, auf einfachste Weise herleiten. Als Beispiel wird eine Strecke der Länge 1 genommen. Sie ist selbstähnlich, da sie aus verkleinerten Kopien ihrer selbst zusammengesetzt werden kann. Dasselbe gilt für ein Quadrat und ebenso für einen Würfel, deren Dimensionen allesamt bereits bekannt sind.

---

---

Die oben abgebildete Einheitsstrecke wurde in vier gleich lange Teile unterteilt, dasselbe gilt für die Seiten des Einheitsquadrates und des Einheitswürfels, d.h. dass der Skalierungsfaktor $s$ jeweils $\frac{1}{4}$ lautet. Nun zähle man die Anzahl der Teilobjekte aus: Die Strecke besteht aus $n=4$, das Quadrat aus $n=4^2=16$ und der Würfel aus $n=4^3=64$ Teilobjekten. Wie unschwer zu erkennen ist, ergibt der Exponent, nennen wir ihn $D$, jeweils die Dimension unserer Probeobjekte an. Daher kann folgende Behauptung aufgestellt werden:

Die Anzahl der Teilobjekte ist also der Kehrwert des Skalierungsfaktors potenziert mit der Dimension des jeweiligen Probeobjektes. Diese Gleichung lässt sich durch Logarithmierung nach $D$ umstellen und man erhält

$$D=\frac{logn}{log\left(\frac{1}{s}\right)}.$$

(16)

Dies ist die Definition der Selbstähnlichkeitsdimenision $D_s$. Sie kann auf alle selbstähnlichen Fraktale angewendet werden. Nun wird versucht, die Dimension der Cesàro-Kurve zu berechnen. Dazu wird zunächst der Fall $\theta =\frac{\pi }{3}$ genommen, also die Koch-Kurve, deren Skalierungsfaktor bereits bekannt ist; er lautet $s=\frac{1}{3}$. Genauso ist bereits bekannt, dass die Koch-Kurve, wie auch jede Cesàro-Kurve, aus vier Kopien ihrer selbst zusammengesetzt ist. Die Selbstähnlichkeitsdimenision beträgt daher

$$D_s=\frac{log4}{log\left({\left(\frac{1}{3}\right)}^{-1}\right)}=\frac{2\cdot log2}{log3}\approx 1,262$$

Diesen Wert kann man als Maß für die "Gebrochenheit", d.h. der komplexen Struktur, die das Fraktal bildet, ansehen.
Nun wird versucht, eine allgemeine Dimensionsgleichung für alle Cesàro-Kurven aufzustellen. Dazu muss die Teilstreckenskalierung anhand des Basiswinkels $\theta$ des gleichschenkligen Dreiecks bestimmt werden.

---

---

Wie der obigen Abbildung leicht zu entnehmen ist, entspricht der Skalierungsfaktor $s$ für die Länge der Teilstrecken $r$ dem Verhältnis der Grundstrecke $2r+x$ und $r$. In Abhängigkeit von $\theta$ ergibt sich folgende Rechnung

Es gilt

$$\frac{1}{s}=\frac{2r+x}{r}$$

sowie

$$cos\theta =\frac{\frac{x}{2}}{r}=\frac{x}{2r}$$

$$\iff x=cos\theta \cdot 2r$$

Nun folgt

$$\frac{1}{s}=\frac{2r+cos\theta \cdot 2r}{r}$$

$$=\frac{2r}{r}+\frac{cos\theta \cdot 2r}{r}=2+2cos\theta =2\left(1+cos\theta \right)$$

$$\iff s=\frac{1}{2\left(1+cos\theta \right)}$$

Nun kann man die fraktale Dimension einer beliebigen Cesàro-Kurve bestimmen

Beispielsweise erhält man für den Fall $\theta =\frac{5\pi }{18}$ einen Wert von $D\approx 1,165$. Für die Grenzfälle $\theta =0$ und $\theta =\frac{\pi }{2}$ erhält man $D=1$ bzw. $D=2$. Die fraktale Dimension der Cesàro-Kurve steigt also mit zunehmendem $\theta$ und nimmt Werte zwischen 1 und 2 an. Die topologisch betrachtet eindimensionale Kurve füllt bei $\theta =\frac{\pi }{2}$ schließlich sogar eine Fläche aus, bildet also ein zweidimensionales Objekt. Daher bezeichnet man die Cesàro-Kurve in diesem Fall auch als Cesàro-Füllkurve, da die sie eine Fläche gänzlich ausfüllt. (Es gibt weitere Fraktale, die ein sehr ähnliches Verhalten zeigen.) Zu beachten ist jedoch, dass die Kurve stets topologisch eindimensional bleibt, und das Bilden einer Fläche nur aus deren besonderen Verhalten resultiert, da die Kurve selbst nie zu einer Fläche wird, sondern theoretisch unendlich dünn bleibt. Ebenso interessant ist der Fall $\theta =0$, bei dem die Kurve die Einheitsstrecke bildet und somit kein Fraktal ist (da keine Skaleninvarianz vorliegt).
Die Cesàro-Kurve ist daher ein ideales Beispiel für die Auswirkungen der Änderung der fraktalen Dimension. Mit Hilfe dieser neuen Definition kann man beliebigen selbstähnlichen Objekten eine bestimmte Dimension zuordnen, die man als ein Maß für die "Zerklüftetheit" bzw. "Rauheit" sowie Komplexität des Fraktales auffassen kann. Natürlich ist eine Dimension, die Werte aus $ℝ$ annehmen kann, nicht besonders intuitiv, jedoch reicht die Betrachtung der topologischen Dimension nicht aus, um ein Fraktal zu beschreiben, da es sich anders verhält als die Objekte der "klassischen Geometrie". Jedoch kann auch die Dimension eines Fraktales durchaus ganzzahlig sein, wie man leicht am Beispiel der Cesàro-Kurve $\theta =\frac{\pi }{2}$ feststellen kann. Eines haben aber alle fraktalen Cesàro-Kurven gemeinsam: Ihre fraktale Dimension $D$ ist stets größer als ihre topologische Dimension $D_T$, d.h., dass

$$D>D_T$$

(17)

gilt. Diese Definition für Fraktale wurde ebenfalls von Mandelbrot eingeführt und lässt sich auf fast alle fraktalen Mengen anwenden. Zwar gibt es wenige Ausnahmen, die sogar selbst Mandelbrot bedauert, jedoch hilft diese Definition, die allermeisten Fraktale, auf die diese zutrifft, von anderen Mengen abzugrenzen. Fakt ist, dass ein Objekt mit einer nicht ganzzahligen Dimension immer ein Fraktal ist. Im Folgenden werden ausschließlich Fraktale behandelt, auf die Mandelbrots Definition zutrifft.

3.3.2 Allgemeine Flächenformel der Cesàro-Kurve

Um noch einmal zu verdeutlichen, dass eine unendlich lange Kurve eine endliche Fläche einschließen kann, soll an dieser Stelle die exakte Fläche berechnet werden, die die Cesàro-Kurve mit der Einheitsstrecke, also ihrem Initiator, einschließt. Dazu ist es zunächst notwendig, die Fläche des gleichschenkligen Dreiecks, das bei der ersten Iteration entsteht, anhand des Basiswinkels $\theta$ zu bestimmen.

---

---

Für die Fläche dieses Dreiecks $A_{△}$ gilt in Abhängigkeit von $\theta$:

$$A_{△}=s\cdot h$$

$$h=sin\theta \cdot c$$

$$s=cos\theta \cdot c$$

$$c=\frac{1}{2\left(1+cos\theta \right)}$$

$$A_{△}=\frac{sin\theta \cdot cos\theta }{4{\left(1+cos\theta \right)}^2}$$

(18)

Interessant ist, dass diese Formel für $\theta =\frac{\pi }{3}$ und variablem $c$ die bekannte Flächenformel für das gleichseitige Dreieck ergibt:

Nun kann man das Verhalten der Flächen während der ersten Iterationen untersuchen:

---

---

 
Während der 1. Iteration beträgt die Fläche der Konstruktionsstufe mit der Initiatorstrecke

---

---

 
Bei der 2. Iteration kommen vier neue Dreiecke hinzu. Somit beträgt die Fläche nun

Entsprechend beträgt sie während der 3. Iteration, bei der $4^2=16$ neue Dreiecke hinzukommen:

Hieraus ergibt sich für die Fläche der Grenzkurve folgende Reihe:

$$A_{\text{Cesàro}}=\sum _{n=0}^{\infty }{4}^n\left({\left(\frac{1}{4{\left(1+cos\theta \right)}^2}\right)}^{n+1}\cdot sin<!--FUNCTION\; APPLICATION-->\theta \cdot cos <!--FUNCTION\; APPLICATION-->\theta \right)$$

Durch Ausmultiplizieren der Konstanten erhält man folgende geometrische Reihe:

$$A_{\text{Cesàro}}=\frac{sin\theta \cdot cos\theta }{4{\left(1+cos\theta \right)}^2}\cdot \sum _{n=0}^{\infty }{\left(\frac{1}{{\left(1+cos\theta \right)}^2}\right)}^n$$

Für den Fall, dass

$$\frac{1}{(1+cos\theta {)}^2}\le 1$$

ist die Reihe konvergent. Da ferner $0\le \theta \le \frac{\pi }{2}$ gelten muss, ist die Konvergenzbedingung somit erfüllt. Folglich erhält man als endgültige Flächenformel der Cesàro-Kurve:

$$A_{\text{Cesàro}}=\frac{sin\theta \cdot cos\theta }{4{\left(1+cos\theta \right)}^2}\cdot \frac{{\left(1+cos\theta \right)}^2}{{\left(1+cos\theta \right)}^2-1}=\frac{sin\theta }{4\left(cos\theta +2\right)}$$

(19)

Um nun beispielsweise die Fläche, die die Koch-Kurve mit der Initiatorstrecke einschließt, zu erhalten, setze man $\theta =\frac{\pi }{3}$:

$$A_{\text{Koch}}=\frac{sin\frac{\pi }{3}}{4\left(cos\frac{\pi }{3}+2\right)}=\frac{\sqrt{3}}{2}\cdot \frac{1}{10}=\frac{\sqrt{3}}{20}$$

Die oben hergeleitete Flächenformel ergibt aufgrund der geometrischen Betrachtungen nur dann Sinn, sofern $0\le \theta <\frac{\pi }{2}$ gilt. Hierbei steigt die Fläche von (logischerweise) $A=0$ bis auf folgenden Grenzwert an:

$$\underset{\theta \to \frac{\pi }{2}}{lim}\frac{sin\theta }{4\left(cos\theta +2\right)}=\frac{1}{8}$$

Im Fall $\theta =\frac{\pi }{2}$ muss aber wiederum $A=0$ gelten, da die Kontur der Kurve nur noch aus Linien, die keine Fläche mehr einschließen können, besteht. Folglich lässt sich die Fläche der Cesàro-Kurve in Abhängigkeit von $\theta$ nur als stückweise Funktion definieren:

$$A_{\text{Cesàro}}\left(\theta \right)=\left\{\begin{array}{cc}\frac{sin\theta }{4\left(cos\theta +2\right)}\hfill & \text{falls }0\le \theta <\frac{\pi }{2}\hfill \\ 0\hfill & \text{falls }\theta =\frac{\pi }{2}\hfill \end{array}\right.$$

(20)

Wie bereits erwähnt, sind die Flächen mit der Initiatorstrecke aller Cesàro-Kurven mit $0<\theta <\frac{\pi }{2}$ endlich, aber ihre Längen stets unendlich. Dieses Paradoxon erschwert es, solche Objekte zu handhaben. Jedoch kann dank der fraktalen Dimension jede dieser Kurven genau charakterisiert werden. Es lässt sich ebenfalls deutlich erkennen, dass mit zunehmender fraktaler Dimension auch die von der Kurve eingeschlossene Fläche ansteigt.

3.4 Weitere klassische Fraktale

Im Folgenden werde werden kurz einige weitere klassische Fraktale vorgestellt. Ein tief gehendes Verständnis der ursprüngliche Gedanken der Mathematiker, die diese entwickelten, ist hier aus Platzgründen aber nicht möglich. Dennoch werden weitere "Anschauungsobjekte" benötigt, insbesondere im Hinblick auf den folgenden Abschnitt.

3.4.1 Das Sierpiński-Dreieck

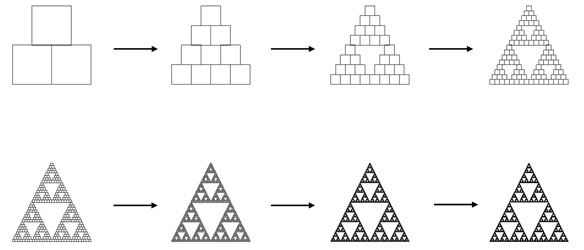
Das Sierpiński-Dreieck wurde 1916 vom polnischen Mathematiker Wacław Sierpiński eingeführt. Es wird konstruiert, indem ein gleichseitiges Dreieck der Seitenlänge 1, dem Generator, in der Mitte ein weiteres Dreieck, deren Eckpunkte die Schnittpunkte der Seitenhalbierenden sind, entfernt wird (Initiator). Es verbleiben drei kongruente und dem Initiatordreieck ähnliche Dreiecke. Dieser Algorithmus wird unendlich oft auf die jeweils verbleibenden Dreiecke angewendet.

---

---

Das bei diesem Verfahren entstandene Fraktal hat keine Fläche, da es sich um einen unendlichen Entfernungsprozess handelt, ⁹ und ist ebenso wie die Koch-Kurve selbstähnlich: Es ist aus drei auf $\frac{1}{2}$ skalierten verkleinerten Kopien aufgebaut. Daher kann man auch hier die fraktale Dimension mit Hilfe der Selbstähnlichkeitsdimension bestimmen:

Das Sierpiński-Dreieck ist also ein Gebilde, dass zwar keine Fläche hat, sich jedoch eher wie ein zwei- als ein eindimensionales Objekt verhält.

3.4.2 Der Sierpiński-Teppich

Dieses Fraktal wurde ebenfalls von Wacław Sierpiński eingeführt. Es beruht ebenso wie sein Dreieck auf einem unendlichen Entfernungsprozess. Hierbei ist jedoch nicht ein gleichseitiges Dreieck, sondern ein Quadrat der Seitenlänge 1 der Initiator. Anschließend wird dieses in neun Teildreiecke geteilt, wovon das mittlere entfernt wird, wobei acht auf $\frac{1}{3}$ skalierte, kongruente und zu Urspungsquadrat ähnliche Teilquadrate übrig bleiben (Generator). Auch hier wird der Generator auf alle diese verbliebenen Quadrate angewendet. Zwar scheinen beide Fraktale einem sehr ähnlichen Konstruktionsprozess zu entstammen, so haben sie jedoch komplett unterschiedliche fraktale Dimensionen. Die Selbstähnlichkeitsdimension des Sierpiński-Teppichs beträgt

und zeigt, dass dieses Fraktal dem Verhalten nach einer Fläche deutlich näher ist als das Sierpiński-Dreieck und von einer weitaus größeren Komplexität ist.

---

---

4 Iterierte Funktionensysteme (IFS)

In diesem Abschnitt werden die sog. iterierten Funktionensysteme (IFS) vorgestellt. Es handelt sich hierbei um ein Verfahren zur Generierung fraktaler Bilder. Anhand der Theorie, die im Folgenden vorgestellt wird, wurde als praktisches Produkt im Rahmen dieser Arbeit ein Computerprogramm entwickelt, das dieses Verfahren implementiert.

4.1 Die Metapher der MVKM

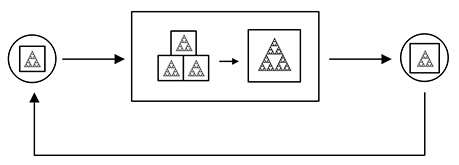
Iterierte Funktionensysteme lassen sich gut mit Hilfe der folgenden Metapher einer sog. Mehrfach-Verkleinerungs-Kopier-Maschine (MVKM) erläutern: Man denke sich eine MVKM als ein Gerät, das aus $n$ Linsensystemen zusammengesetzt ist, wobei jedes dieser Linsensysteme Bilder unterschiedlich stark kontrahiert und unabhängig ist, d.h., die Eingabe, die das System erhält, nicht von den anderen beeinflusst wird. Dabei kann die Anordnung dieser Systeme innerhalb der Maschine beliebig sein. Nimmt man nun ein beliebiges Anfangsbild $A_0$, so wird dieses kopiert und durch die Linsensysteme geschickt. Diese erzeugen jeweils eine verkleinerte Ausgabe des Ursprungsbildes. Alle diese Ausgaben werden nun zu einem einzigen Ausgabe-Bild zusammengesetzt, d.h. die Ausgabe ist eine "Collage" der jeweiligen Linsenausgaben entsprechend deren Anordnung. Nun befindet sich die Maschine in einer Rückkoppelungsschleife, ¹⁰ d.h. dass ihre Ausgabe ihr wieder als Eingabe zugeführt wird. Führt man diese Rückkoppelung unendlich oft aus, so erhält man eine Ausgabe $A_{\infty }$, die unabhängig von dem Anfangsbild $A$ ist. Ausschließlich die Anordnung der Linsensysteme ist für das Aussehen dieser als Attraktor der MVKM bezeichnete Ausgabe verantwortlich. Der Attraktor ist ein Zustand, gegen den das Rückkoppelungssystem immer streben wird. Nimmt man als Anfangsbild den Attraktor, so kommt es zu keiner Veränderung der Ausgabe. Es folgt eine Abbildung, die den Grundaufbau einer MVKM darstellt.

---

---

Eine MVKM ist eine Rückkoppelungsmaschine: Links ist die sog. Eingabeeinheit, in diesem Fall ein beliebiges Bild. Die Eingabe wird an die Prozessoreinheit übergeben, wo jede Kopie des Eingabebildes entsprechend dem Linsensystem verändert ¹¹ und zu einer Collage zusammengesetzt wird. Anschließend wird das Bild der Ausgabeeinheit übergeben. Diese wiederum übergibt die Ausgabe an die Eingabeeinheit über die sog. Rückkoppelungsleitung.

---

---

Wie in der obigen Abbildung leicht zu erkennen ist, lässt diese spezielle MVKM ihren Attraktor unverändert. Der Attraktor der obigen MVKM ist in diesem Fall übrigens das Sierpiński-Dreieck! Dies ist kein Zufall, denn MVKMs haben in der Regel Fraktale als Attraktoren. ¹²
Die MVKM ist daher eine geeignete Metapher für das Konzept der iterierten Funktionensysteme, das durch den Mathematiker John Hutchinson im Jahr 1981 entwickelt wurde.

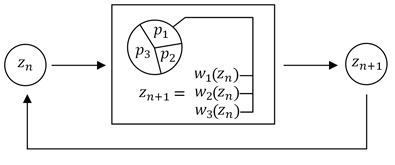
4.2 Definition von IFS

Nun kommen wir zur mathematischen Beschreibung von IFS:
Ein IFS ist gegeben durch eine Menge $F$ von $N\in \mathbb{N}$ Kontraktionen $w_n$ eines vollständigen metrischen Raumes $X$ auf sich selbst, d. h. Bild- und Urbildpunkte der Abbildungen liegen im selben Raum:

$$F=\left\{w_n:X\to X|n=1,2,...,N\right\}$$

(21)

Diese Kontraktionen stellen metaphorisch die Linsensysteme der MVKM dar. Es kann sich dabei um eine beliebige Kontraktion handeln, der Einfachheit wegen beschränken wir uns jedoch ausschließlich auf affine Abbildungen; theoretisch wären aber genauso auch andere Arten von Abbildungen möglich. Es wurde gezeigt, dass die MVKM alle Abbilder der Linsensysteme zu einem Ausgabebild zusammengefügt hat. Mathematisch betrachtet handelt es sich um die Abbildung $W\left(A\right)$ durch Vereinigung der jeweiligen Bildmengen, die durch eine der $n$ Abbildungen auf die Ausgangsmenge $A$ erzeugt wurden, formal

$$W\left(A\right)=w_1\left(A\right)\cup w_2\left(A\right)\cup \cdots \cup w_n\left(A\right)=\bigcup _{n=1}^N{w}_n\left(A\right).$$

(22)

$W\left(A\right)$ wird als Hutchinson-Operator bezeichnet. Er kann als die Prozessoreinheit der MVKM angesehen werden. Der Hutchinson-Operator wird nun auf eine beliebige Anfangsmenge $A_0$ angewendet, wobei die erste Ausgabe der MVKM entsteht: $A_1=W\left(A_0\right)$. Da es sich aber um ein Rückkoppelungssystem handelt, kann die Ausführung der MVKM als Iteration des Hutchinson-Operators angesehen werden:

$$A_{n+1}=W\left(A_n\right)$$

(23)

Die Ausgabe des Operators wird ihm also wieder als Eingabe zugeführt, genauso wie bei der MVKM. Iteriert man dieses System nun unendlich oft, so wird es stets immer gegen den stabilen Zustand, den Attraktor $A_{\infty }$ des IFS, streben. Dabei gilt wie erläutert

$$A_{\infty }=W\left(A_{\infty }\right),$$

(24)

d.h. dass der Hutchinson-Operator den Attraktor unverändert (invariant) lässt. Daher wird $A_{\infty }$ auch als Fixpunkt des IFS bezeichnet. Zu beachten ist, dass ein IFS nur einen einzigen Attraktor haben kann, und dieser ist in der Regel fraktal. Diese Eigenschaft kann genutzt werden, um durch eine gegebene Anzahl von affinen Abbildungen ein Fraktal kodieren und generieren zu können. Das IFS strebt deshalb immer zu dem Attraktor, weil die verwendeten Abbildungen Kontraktionen sind, demnach auch der Hutchinson-Operator selbst. Dadurch lässt sich das Banachsche Fixpunktprinzip aufgreifen: Das System wird immer einen eindeutigen Fixpunkt haben.

4.3 Kodierung von Fraktalen durch IFS

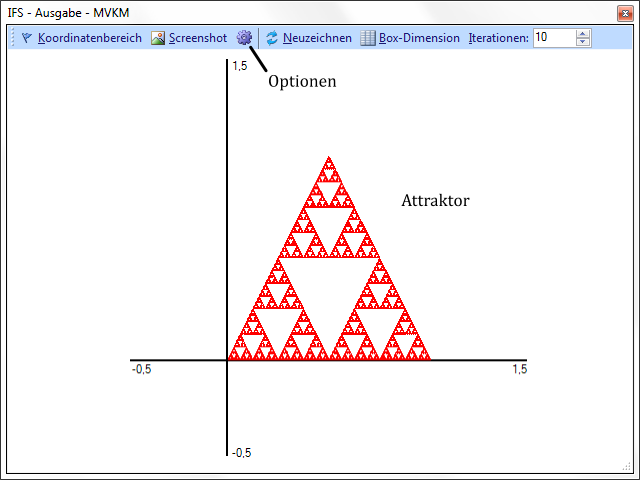
Im Folgenden werden die Kodierung und Generierung von Fraktalen durch IFS erläutert. Der Attraktor dieser IFS wird dann stets das gegebene Fraktal sein. Da viele Fraktale selbstähnlich sind, lassen sie sich durch die Ähnlichkeitsabbildungen, die ihr Ganzes auf ihre Teile abbilden, kodieren. Als Beispiel nehmen wir das Sierpiński-Dreieck. Es ist wie bekannt aus drei selbstähnlichen Teilen aufgebaut, daher kann es durch ein IFS mit den folgenden affinen Abbildungen dargestellt werden:

Die Iteration des Hutchinson-Operators $W\left(A\right)=w_1\left(A\right)\cup w_2\left(A\right)\cup w_3\left(A\right)$ auf ein beliebiges Startbild $A_0$ führt stets zu diesem Fraktal als Attraktor. Die affinen Abbildungen, die zur Beschreibung des Sierpiński-Dreiecks notwendig sind, wurden durch ihre Eigenschaft der Selbstähnlichkeit bestimmt: Man benötigt drei Ähnlichkeitsabbildungen, die das gesamte Fraktal jeweils auf eines ihrer ähnlichen Teile abbilden, z.B. bildet $w_3$ das Dreieck auf den unteren linken Teil ab. Da IFS aber auch die allgemeineren affinen Abbildungen zulassen, lassen sich nicht nur selbstähnliche, sondern auch sog. selbstaffine Fraktale kodieren. Sie sind aus affinen Kopien, analog zu den selbstähnlichen Fraktalen, ihrer selbst zusammengesetzt. Fakt ist, dass jedes Fraktal, das aus selbstähnlichen oder selbstaffinen Kopien zusammengesetzt ist, ein Attraktor eines IFS ist.
Genauso wie man bereits vorhandene Fraktale kodieren kann, lassen sich mit IFS also auch komplett neue Fraktale durch beliebige Variation von kontrahierenden affinen Abbildungen erzeugen, die allgemein als IFS-Fraktale bezeichnet werden.
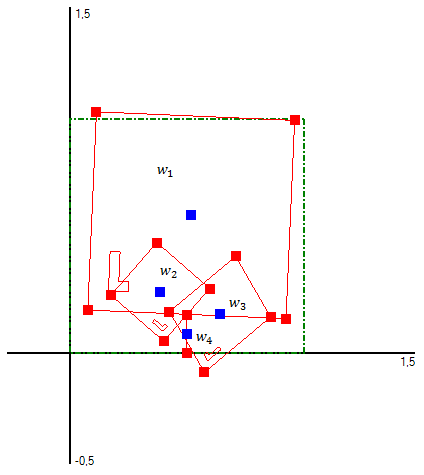
Um diese affinen Abbildungen auf eine einfache Weise bestimmen zu können, kann man sie durch ein Urbildparallelogramm und mehrere Abbildparallelogramme grafisch repräsentieren lassen. Durch Anwendung verschiedener affiner Abbildungen wie Translation oder Skalierung auf ein vorher definiertes Urbildparallelogramm lassen sich verschiedene Parallelogramme erzeugen, die jeweils eine affine Abbildung repräsentieren, nämlich diejenige, die das Urbildparallelogramm auf das entsprechende Abbildparallelogramm abbildet. Somit können auf eine sehr intuitive Weise beliebige affine Abbildungen definiert werden.
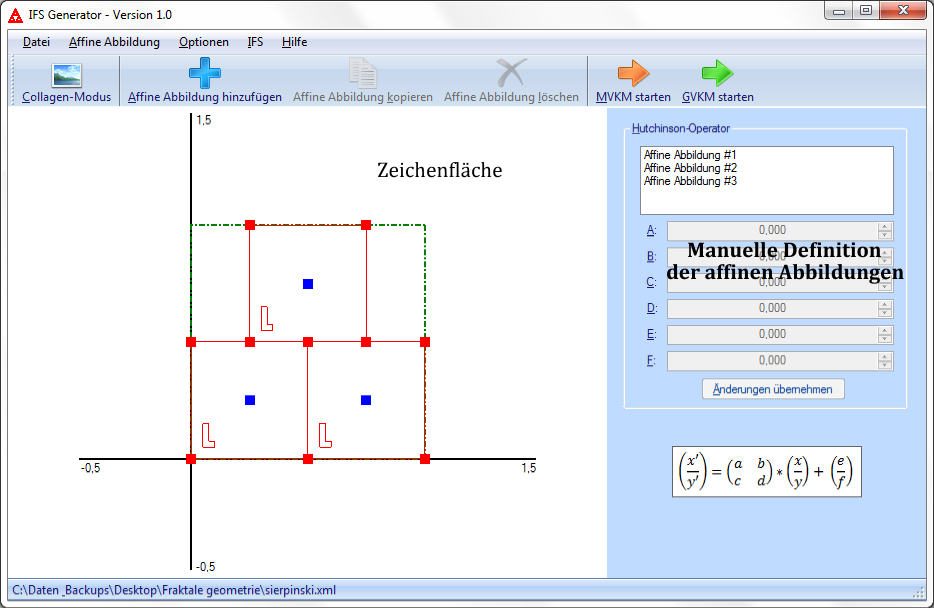
Dieses sehr anschauliche Konzept verfolgt auch das Programm IFS-Generator: Im Hauptfenster befindet sich die Zeichenfläche, auf der sich das Urbildparallelogramm, hier ein Quadrat, befindet. Erstellt man nun eine neue affine Abbildung, so wird zunächst eine 1:1-Kopie des Urbildparallelogrammes erstellt, die Abbildung, die dadurch repräsentiert wird, ist daher:

$$w=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)\cdot \overrightarrow{x}$$

Nun lässt sich dieses Parallelogramm mit dem Programm auf die durch affine Abbildungen definierte Art und Weise transformieren. Das Programm bestimmt anschließend aus drei Punkten des Urbildparallelogrammes und der jeweiligen Abbildparallelogramme die entsprechenden affinen Abbildungen, die durch jene repräsentiert werden.

---

---

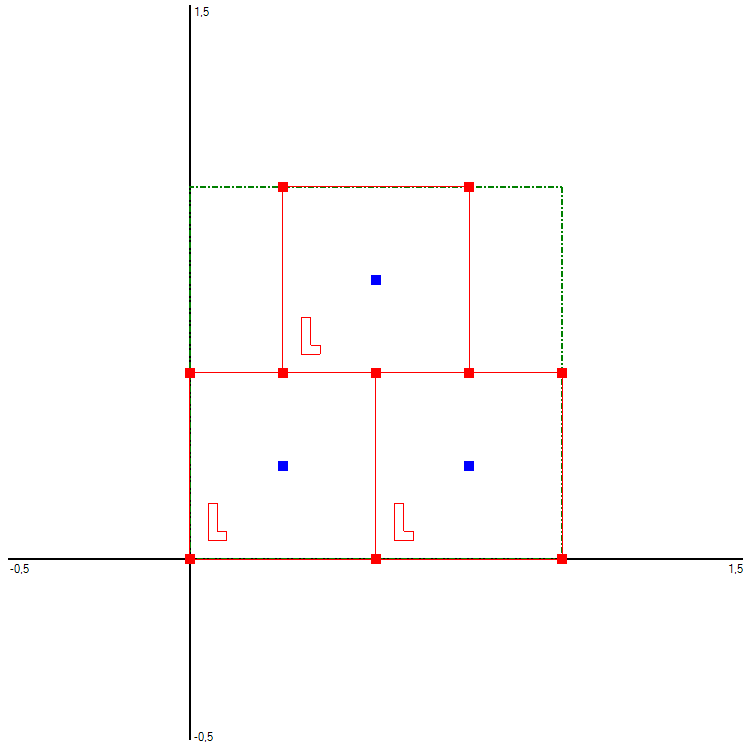
Die Abbildparallelogramme enthalten zusätzlich ein einbeschriebenes "L", um bei Spiegelungen und Rotationen eindeutig zu sein. Ansonsten könnten diese Abbildungsarten nicht unterschieden werden.
Natürlich kann der Hutchinson-Operator in der Praxis nicht unendlich oft iteriert werden. In der Regel reichen bereits 10 Iterationen aus, um eine gute Näherung erhalten zu können. Zwar kann das Startbild $A_0$ theoretisch beliebig sein, jedoch wäre es jedoch sehr unpraktisch, dieses einzulesen, dann zu transformieren und dies mit der Ausgabe ständig zu wiederholen.
Stattdessen wird folgender Algorithmus verwendet, der durch Berechnen und Zeichnen von Parallelogrammen eine Näherung des Attraktors erzeugt: Man geht von den Eckpunkten
$A\left(0|1\right),B\left(0|0\right),C\left(1|0\right)\mathrm{\text{und }}D\left(1|1\right)$ eines Quadrats aus. Auf diese vier Punkte werden jeweils die $n$ gegebenen affinen Abbildungen angewendet, wodurch man die Eckpunkte von $n$ neuen Bild-Parallelogrammen erhält, dabei ersetzt man die Koordinaten des Urbild-Parallelogramms durch die gerade berechneten. Dieses Verfahren wird rekursiv auf alle entstandenen Parallelogramme angewendet. Dabei entspricht eine Rekursion jeweils einer Iteration des Hutchinson-Operators. Nach einer vorher definierten Zahl von Iterationen werden aus den berechneten Eckpunkten die Parallelogramme auf der Ausgabefläche gezeichnet und das Verfahren abgebrochen. ¹³

---

---

4.4 Fraktale Modellierung mit Hilfe von IFS

Bisher wurden ausschließlich die klassischen Fraktale behandelt, die zwar eine komplexe, aber nicht naturähnliche Form haben. Jedoch gibt es nicht nur in der Mathematik skaleninvariante und selbstaffine Strukturen, sondern auch in der Natur. Natürlich ist dort der Grad an Skaleninvarianz begrenzt, dennoch ist z.B. ein Farnblatt aus vielen Unterblättern aufgebaut, die dem ganzen Blatt recht ähnlich sehen. Weitere skaleninvariante Systeme wären beispielsweise auch eine Wolke oder ein Baum. Der Begründer der modernen Fraktalgeometrie Mandelbrot erkannte, dass fast alle natürlichen Strukturen fraktale Muster zeigen. Solche Systeme werden daher als natürliche Fraktale bezeichnet. Am Beispiel der IFS soll im Folgenden gezeigt werden, wie man natürliche Bilder in einem gewissen Grad als ein Fraktal darstellen (kodieren) kann.

---

---

Der Mathematiker Michael Barnsley entwickelte eine Methode, mit der man viele vorhandene Bilder in ein IFS "umwandeln" kann. Dafür entwickelte er den sog. Collagen-Satz. Dieser besagt, dass man ein beliebiges Bild derart mit affinen Kopien seines selbst überdecken soll, sodass alle diese Kopien eine Collage des Ursprungsbildes bilden. Die affinen Abbildungen, die das Urbild auf die Kopien abbilden, bilden dann den Hutchinson-Operator des IFS. Dieses IFS wird nun als Attraktor in etwa das Bild erzeugen, das man als Vorlage verwendet hat. Natürlich lässt sich dieses interessante Verfahren nur auf solche Bilder anwenden, die bereits eine annähernd selbstaffine Struktur besitzen. Um die Methode auf eine sehr einfache Art durchzuführen, bietet es sich an, ein Computerprogramm zu verwenden, das ein gegebenes Bild einliest und daraus Kopien erstellt, die man auf dem Bildschirm gemäß des Collagen-Satzes anordnen kann.
Barnsley wandte sein Verfahren u.a. auch auf einen Farn an. Ergebnis ist das folgende IFS mit nur vier affinen Abbildungen (das als Barnsley-Farn bezeichnet wird):

Nun wird versucht, dieses IFS mit der oben erläuterten Methode darzustellen. Dazu wird eine Anzahl von $n_i=10$ Iterationen gewählt. Ergebnis ist die folgende Ausgabe:

---

---

Das Bild lässt bereits die Mächtigkeit von IFS zur Darstellung natürlicher Strukturen erkennen, dennoch scheint die Methode nicht zu dem gewünschten Ergebnis geführt zu haben. Man erkennt immer noch die einzelnen Parallelogramme, die das Programm gezeichnet hat. Tatsächlich ist es so, dass nicht nur 10, sondern etwa 50 Iterationen notwendig wären, um diesen Attraktor darzustellen. Dies wäre jedoch nicht performant, da die Anzahl an zu zeichnenden Parallelogrammen mit jeder Iteration ansteigt, was eine sehr rechenaufwendige Methode darstellen und eine sehr lange Berechnungszeit erfordern würde. Der Grund für dieses Verhalten sind die starken Differenzen bei den Kontraktionsfaktoren der affinen Abbildungen, sodass die Parallelogramme pro Iteration nur sehr langsam an Größe abnehmen. Das Problem der hinreichenden Darstellung eines Attraktors wird auch als Dekodierungs-Problem bezeichnet. Der bisherige Algorithmus ist also nicht geeignet, um alle Attraktoren generieren zu können.

4.5 Der Chaosspiel-Algorithmus

Um das Dekodierungs-Problem zu lösen, wurde der sog. Chaosspiel-Algorithmus eingeführt. Es handelt sich dabei um eine erstaunliche Methode, um performant eine Näherung des Attraktors eines IFS generieren zu können. Diese neue Methode lässt sich metaphorisch durch eine sog. Glücksrad-Verkleinerungs-Kopier-Maschine (GVKM) erläutern: Diese neue Art von Kopiermaschine arbeitet nicht mehr mit einem Anfangsbild, sondern einem einzigen Anfangspunkt. Sie wählt im Gegensatz zur MVKM ein Linsensystem zufällig mit einer bestimmten Wahrscheinlichkeit $p_n$ aus und wendet es auf diesen Punkt an. Dabei erhält man einen neuen Punkt, den die Maschine auf ein Papier zeichnet. Anschließend wird dieses Verfahren auf diesen neu erhaltenen Punkt wiederholt angewandt.

---

---

Die GVKM ist wie die MVKM ein Rückkoppelungssystem: Der Anfangspunkt $z_n$ wird durch eine zufällig mit der Wahrscheinlichkeit $p_n$ ausgewählte affine Abbildung $w_n$ auf den nächsten Punkt $z_{n+1}$ abgebildet. Anschließend wird dieser der Maschine wieder als Eingabe zugeführt. Nach vielen Tausenden Iterationen bildet sich der Attraktor des entsprechenden IFS aus.
Dieses Verfahren unterscheidet sich grundlegend vom bisherigen deterministischen Algorithmus, der bei gleichen Anfangsbedingungen stets dasselbe Ergebnis liefert. Das Chaosspiel erzeugt dagegen eine zufällige Folge von Punkten, die aber dennoch gegen den Attraktor strebt. Diese Methode wird in der Mathematik als zufällig iteriertes Funktionensystem bezeichnet und ist eine der geeignetsten Methoden, Attraktoren von IFS zu erzeugen. Die Erklärung, warum die Punktfolge gegen den Attraktor konvergiert, würde den Rahmen dieser Arbeit sprengen. Es sei aber zu erwähnen, dass dies nur aufgrund der kontrahierenden Eigenschaften der affinen Abbildungen möglich ist.
Algorithmisch wendet man das Chaosspiel an, indem ein beliebiger Punkt $z_0$ als Startpunkt gewählt wird. Am geeignetsten ist jedoch ein Fixpunkt der verwendeten affinen Abbildungen, da es sonst zu Punkten kommt, die nicht zum Attraktor gehören, weil die entstehende Punktfolge nicht sofort konvergieren würde. Anschließend wird mit einer Zufallsfunktion eine Zahl zwischen 0 und 1 bestimmt. Um die unterschiedlichen Wahrscheinlichkeiten zu beachten, wird geprüft, ob die Zufallszahl kleiner einer der vorher gewählten Wahrscheinlichkeiten ist, ¹³ z.B. wird die affine Abbildung $w_n$ mit der Wahrscheinlichkeitsangabe $p_n$ dann ausgewählt, wenn die Zufallszahl $<p_n$ ist. Nun wird $w_n$ auf $z_0$ angewandt und der entstandene Punkt $z_{n+1}=w_n\left(z_n\right)$ gespeichert bzw. gezeichnet. Anschließend wird diese Methode $N\in \mathbb{N}$ mal iteriert. Nach etwa $N=100000$ Iterationen erhält man eine sehr gute Näherung des Attraktors in performanter Zeit. ¹⁵
Nun wird versucht, diesen Algorithmus auf den Barnsley-Farn anzuwenden. Dazu werden für alle affinen Abbildungen zunächst gleiche Wahrscheinlichkeiten ($p=0,25$) bei einer Anzahl von $N=100000$ Iterationen verwendet.

---

---

Wie unschwer zu erkennen ist, hat diese Methode nicht zu einem optimalen Ergebnis geführt. Um den Farn bei dieser Iterationsanzahl korrekt darzustellen, muss man die Wahrscheinlichkeiten, mit der die jeweiligen Abbildungen ausgewählt werden, anpassen. Dies bewirkt, dass die bisher wenig getroffenen Bereiche des Attraktors häufiger getroffen werden und dieser vollständig sichtbar wird. Dazu kann man sich als Faustregel merken: Die Verteilung der Wahrscheinlichkeiten entspricht in etwa der der Fläche, die die Abbild-Parallelogramme (bei dem oben vorgestellten Verfahren) einnehmen.

---

---

Nun können die Wahrscheinlichkeiten bestimmt werden, sie lauten in etwa $p_1=0,8;p_2=0,1;p_3=0,09\mathrm{\text{ und }}{p}_4=0,01$. Es handelt sich jedoch nur um eine "Methode durch Ausprobieren". Es gibt zwar eine mathematische Näherungslösung, diese ist jedoch zu aufwendig für einfache Experimente (eine optimale Lösung ist auch algorithmisch nicht zu erreichen). Startet man nun die GVKM, so erhält man eine eindrucksvolles Fraktal, das dem Naturvorbild sehr nahe kommt.

---

---

4.6 Die Box-Dimension $D_B$

Zum Schluss soll noch kurz erläutert werden, wie man bei IFS-Fraktalen die fraktale Dimension bestimmen kann. Da bei Weitem nicht alle selbstähnlich sind, kann nicht auf die Selbstähnlichkeitsdimension zurückgegriffen werden. Stattdessen wird die allgemeinere Box-Dimension $D_B$ verwendet. Man erhält sie, indem man über das Bild des Attraktors ein Gitternetz einer beliebigen Maschenweite $s_1$ legt und alle $N_1$ Maschen bzw. Boxen auszählt, die vom Attraktor getroffen wurden. Anschließend verringert man die Maschenweite $s_2$ und zählt erneut alle vom Attraktor getroffenen Maschen $N_2$ aus. Die Box-Dimension beträgt dann

$$D_B=\frac{log{N}_2-log{N}_1}{log\frac{1}{s_2}-log\frac{1}{s_1}}.$$

(25)

Die Box-Dimension ist weniger exakt als die Selbstähnlichkeitsdimension, lässt sich jedoch besonders einfach algorithmisch berechnen, da das Maschenzählen dem Zählen von Pixeln einer Bitmapgrafik entspricht. Beispielsweise erhält man für den Farn dadurch eine fraktale Dimension von $D_B\approx 1,81$. Die Box-Dimension erlaubt es, den Komplexitätsgrad jedes beliebigen Attraktors zu bestimmen. Man geht sogar so weit, dass man sie auf natürliche Fraktale anwendet, z.B. auf Küstenlinien. Sie haben ein ähnliches Verhalten wie die Koch-Kurve, denn umso genauer man sie misst, desto länger wird ihre Gesamtlänge.

4.7 Ausblick

Die IFS sind eine sehr mächtige Methode zur Kodierung fraktaler Bilder. Es ist mit ihnen ebenfalls problemlos möglich, bereits vorhandene Strukturen aus der Natur mathematisch modellieren und am Computer simulieren zu lassen. Man konnte deutlich erkennen, dass die Struktur einer derart komplexen Pflanze wie des Farns durch nur vier affine Abbildungen kodiert werden konnte, was äußerst erstaunlich ist, wenn man beachtet, wie wenig Information aus Sicht des IFS benötigt wird. Die sich daraus ergebenden Anwendungsmöglichkeiten sind sicherlich sehr vielfältig. So wurden IFS bereits zu einer sehr effektiven Komprimierungsmethode weiterentwickelt. Es kann daher auch in Zukunft davon ausgegangen werden, dass die Forschung an diesem relativ neuen Feld weiter vorangetrieben wird.

5 Eigene Wertung

Die fraktale Geometrie ist ein sehr interessantes, jedoch auch sehr umfangreiches Teilgebiet der Mathematik. Im Rahmen dieser Arbeit war es daher nur möglich, einen Bruchteil der Thematik zu behandeln. So war es beispielsweise nicht möglich, auf den Bezug zur Chaostheorie sowie die Mandelbrot- und Juliamengen einzugehen. Dennoch hoffe ich, durch Betrachtung der Arbeiten von Koch, Cesàro, Sierpiński, Mandelbrot, Hutchinson und Barnsley ein grundlegendes Verständnis der Konzepte dieser neuen Art von Geometrie vermittelt zu haben.
Die Recherche zu den Themen sowie die Erstellung des Programmes IFS-Generator erforderte ein hohes Maß an Selbstständigkeit sowie die Fähigkeit zum Autodidaktimus. Ich bin überzeugt, durch diese Besondere Lernleistung einen wichtigen Schritt für ein eventuelles Studium getätigt zu haben.
Insgesamt habe ich sehr viel Interessantes und weit über den Rahmen des Schulunterrichts hinaus Gehendes gelernt und anwenden können.Daher bin ich äußerst zufrieden über die Tatsache, diese Arbeit durchzuführen.

Flensburg, im März 2011

Adrian Jablonski

6 Anhang

6.1 Das Programm IFS-Generator

Im Rahmen dieser Arbeit ist das Programm IFS-Generator entstanden. Es implementiert die Funktionalität der oben erläuterten IFS. Die graphische Oberfläche der Software ist aus einem Zeichenfeld (DrawPanel) und aus einem Ausgabefeld (OutputPanel) aufgebaut.
Im Zeichenfeld können gemäß der im Hauptteil beschriebenen Methode Abbildparallelogramme erstellt werden, die jeweils eine affine Abbildung repräsentieren, und somit ein intuitives Definieren des Hutchinson-Operators erlauben. Dabei kann jedes dieser Parallelogramme im Programm an sog. Anfass-Punkten ¹⁴ mit der Maus transformiert werden, wodurch sich ebenfalls die repräsentierte affine Abbildung ändert. Dabei ist jedoch zu beachten, dass IFS-Generator nicht prüft, ob es sich dabei um eine Kontraktion handelt, da der rechnerische Aufwand zu groß wäre. Stattdessen kann man sich als einfache Regel merken: Eine Abbildung ist mindestens dann eine Kontraktion, wenn sich das Abbildparallelogramm innerhalb des Urbildparallelogramms befindet. Nachdem man die Abbildparallelogramme erstellt hat, werden aus drei Punkten des Urbildparallelogramms und jeweils drei Punkten eines Abbildparallelogramms zwei lineare Gleichungssysteme gemäß Formel 12 aufgestellt und mit Hilfe des Gaussschen Algorithmus gelöst, wodurch man die Elemente der Abbildungsmatrix und des Translationsvektors erhält, die die durch das Parallelogramm repräsentierte affine Abbildung bilden.
Diese affinen Abbildungen werden dann an das Ausgabefeld übergeben. Dieses bietet die Möglichkeit, den Attraktor des IFS entweder durch Verwendung des deterministischen ("MVKM starten") oder des Chaosspiel-Algorithmus ("GVKM starten") zu berechnen. Dabei kann die Farbe, in der dieser dargestellt werden soll, frei gewählt werden. Darüber hinaus bietet das Ausgabefeld die Möglichkeit, im Chaosspiel-Modus für jede verwendete affine Abbildung des Hutchinson-Operators eine eigene Zufallsfarbe zuzuweisen, wodurch man erkennen kann, welche Abbildung für welchen Punkt verantwortlich ist. Ferner wird ebenfalls die Bestimmung der Box-Dimension des gezeichneten Attraktors, das Abspeichern der Parameter sowie das Erstellen von Screenshots unterstützt.
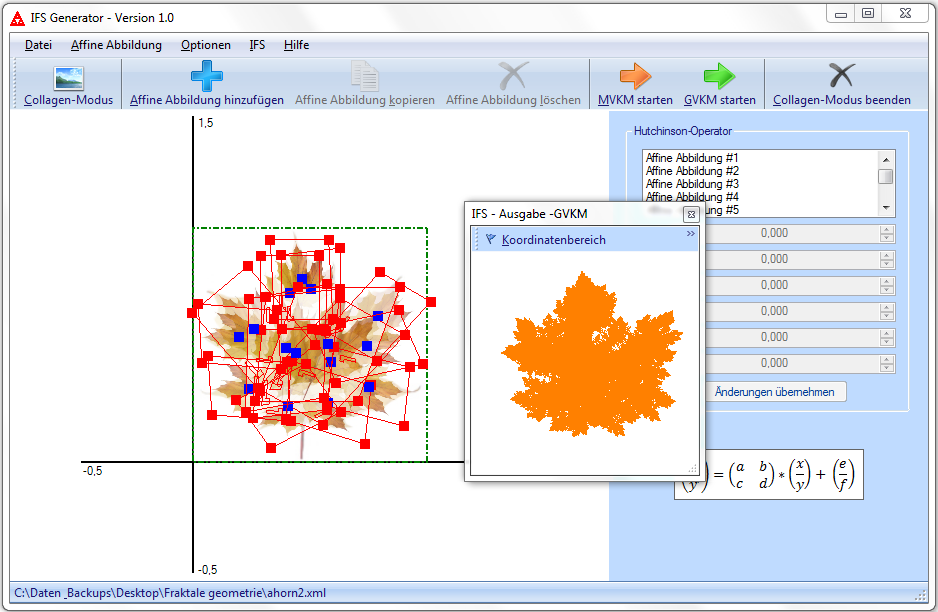
Eine besondere Funktion des Programmes ist jedoch der Collagen-Modus. Er erlaubt es, gemäß dem Collagen-Satz von Barnsley, ein gegebenes Bild in ein IFS zu kodieren. Dazu lädt man das Bild in die Zeichenfläche, wo man es durch affine Kopien seiner selbst komplett überdecken kann. Wenn man anschließend den Attraktor zeichnen lässt, sollte in etwa das gegebene Bild dargestellt werden (natürlich nur einfarbig).
Es folgen einige Screenshots der Software:

---

---

---

---

---

---

6.2 Literaturverzeichnis

[Barn95]	Barnsley, Fraktale, Spektrum Akademischer Verlag, Heidelberg, 1995
[Baum01]	Baum, Lind, Schermuly u.a., Lineare Algebra mit analytischer Geometrie (Leistungskurs), Ernst Klett Verlag, Stuttgart, 2001
[Peit92]	Peitgen, Jürgens, Saupe, Bausteine des Chaos: Fraktale, Springer-Verlag Berlin, und Klett-Cotta, Stuttgart, 1992
[Mand91]	Mandelbrot, Die fraktale Geometrie der Natur, Birkhäuser Verlag, Basel, 1991
[Gruh06]	Gruhn, Jozbasic, Aus der Schulgeometrie: Definition und Klassifikation von Kongruenzabbildungen, Ähnlichkeitsabbildungen und Affinen Abbildungen, Universität Hamburg, http://www.math.uni-hamburg.de/home/koch/lehre/sose06/psem_frak_geom/Aus_der_Schulgeometrie.pdf (30. November 2010)
[Spre09]	Sprengler, Affine Abbildungen im ${ℝ}^2$, Gymnasium Hammerskeil, http://www.mspengler.de/BAUSTELLE/pdf2HP/AffinSkript.pdf (26. November 2010)
[Reit06]	Reiter, Die Ästhetik der Fraktale, 2006, http://www.zonk.at/fraktale/rafael_reiter_die_aesthetik_der_fraktale.pdf (03. November 2010)
[WP1]	Wikipedia, Diskrete Topologie, http://de.wikipedia.org/wiki/Diskrete_Topologie (24. Januar 2011)
[WP2]	Wikipedia, Fraktale Dimension, http://de.wikipedia.org/wiki/Fraktale_Dimension (30. Januar 2011)
[WP3]	Wikipedia, Dimension (Mathematik), http://de.wikipedia.org/wiki/Dimension_(Mathematik) (30. Januar 2011)
[WP4]	Wikipedia, Lebesgue’sche Überdeckungsdimension, http://de.wikipedia.org/wiki/Lebesgue'sche_Überdeckungsdimension (30. Januar 2011)
[WP5]	Wikipedia, Fraktal, http://de.wikipedia.org/wiki/Fraktal (3. November 2011)
[WP6]	Wikipedia, Abgeschlossene Menge, http://de.wikipedia.org/wiki/Abgeschlossene_Menge (6. März 2011)
[WP7]	Wikipedia, Iterated Function System,http://en.wikipedia.org/wiki/Iterated_function_system (23. Februar 2011)

6.3 Bildnachweise

Abb. 4	[Barn95] S. 86
Abb. 21	http://www.flickr.com/photos/white_hamster/3320963199/ (14. März 2011)

---